3.较复杂的求一个数是另一个数的几分之几或百分之几的应用题。

　　这类应用题是简单(基本)应用题的组合或引伸，关键在于找准标准量，并揭示它的变化和其它隐蔽的条件，化繁为简。

　　例1.某班有学生50人，会游泳的有36人，占全班人数的百分之几?如果这个班有女同学25人，其中3/5会游泳，那么，男同学有百分之几会游泳?

　　解：(1)36÷50=72%

　　(2)“男同学中有百分之几会游泳”就是求男同学中会游泳的占男同学的百分之几。应以男同学总数作为标准量。其中会游泳人数作为比较量。但这两个数都要通过已知条件算出来。即：男生人数：50-25=25(人)，男同学中会游泳的人数：36-25×3/5=21(人)，男生有百分之几会游泳：21÷25=84%

　　答：会游泳的占全班人数的72%，男同学中有84%会游泳。

　　例2.某校去年有女生200人，男生比女生多80人。今年女生人数比去年增加20%，因此比男生多30人，今年男生比去年减少百分之几?

　　解：去年女生200人，今年增加了20%，那么今年女生人数是去年的(1+20%)。要求今年男生人数比去年减少了百分之几，应以去年男生人数(200+80)为标准量;以今年(女生人数-30)比去年减少的男生数为比较量。即：200×(1+20%)=240(人)今年女生数。

　　[(200+80)-(240-30)] ÷(200+80)=(280-210)÷280=70÷280=25% 答：今年男生比去年减少了25%。

　　例3.某工厂两个生产小组按计划每月共生产零件680个。结果第一组超额本小组计划的20%，第二组比本组计划多生产零件54个。这样，两个小组比原计划共多生产零件118个。问第二组比本组计划超额百分之几?

　　解：“求第二组比本组计划超额百分之几”实质上也属于求“甲(大数)数比乙(小数)多百分之几”的类型，标准量应是第二组计划生产的零件数。

　　由题意知“两组共多生产零件118个”。而其中又知“第二组多生产54个”。所以，第一组多生产的零件数是118-54=64(个)，是第一组超额部分，相当于第一组计划的20%。所以第一组计划生产零件数是64÷20%=320(个)。那么第二组计划生产零件数则是680-320=360(个)。求出了标准量。再求54(个)占360(个)的百分之几，就是求比计划超额的百分数。即：54÷360=15%。

　　综合式：54÷[680-(118-54)÷20%]=54÷[680-64÷20%]=54÷[680-320]=54÷360=15%

　　答：第二组比本组计划超额15%。

　　4.较特殊的求一个数是另一个数的几分之几(百分之几)的应用题。

　　这类应用题一般数量关系抽象复杂，解法一般不符合基本题的关系式，要具体问题具体分析。

　　例1。某校五年级学生人数的2/3等于四年级学生人数的4/5，问五年级人数是四年级学生人数的几分之几?四年级学生人数是五年级学生人数的几分之几?

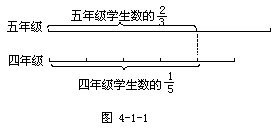
　　解：(1)五年级学生人数的1/3=四年级学生人数的4/5÷2=4/5×1/2。所以，五年级学生人数是四年级学生人数的：4/5×1/2×3=6/5 (2)同理，四年级学生人数是五年级学生人数的：2/3÷4/5=5/6 答：(略)

　　说明：一般来说，若甲数的a/b等于乙数的c/d，则甲数就是乙数的c/d÷a/b。乙数就是甲数的a/b÷c/d(a、b、c、d≠0)。如果甲数是乙数的m/n，则乙数就是甲数的n/m。但如果求的是百分数，其形式看上去不同，实际是一样的。一般的说，甲数的a%等于乙数的b%，则甲数就是乙数的b/a×100%;乙数就是甲数的a/b×100%。所以在运算时，只用百分数的分子进行运算就可以了。

　　例2.甲数比乙数少37.5%，乙数比甲数多百分之几?

　　甲数比乙数多15%，乙数比甲数少百分之几?

　　解：第一问应以甲数为标准量，第二问也应以甲数为标准量。问题在于怎样表示甲、乙二量以及它们的差量，必须正确理解题意。

　　“甲数比乙数少37.5%”这句话是以乙为标准量，为了简便设乙为100，则甲数应该是100-37.5=62.5。所以第一问可以用(乙-甲)÷甲=37.5÷(100-37.5)=60%来表示得数。

　　“甲比乙多15%”这句话，如以乙为标准量时则甲=乙+ 15(设乙为100)，则乙比甲少15。所以第二问可以用(甲-乙)÷甲=15÷(100+15)=13.04%来表示得数。

　　这个求法，是省略了分母100的简略写法。当甲是小数时，所求的百分比是差量÷(1-差量)×100%;当甲是大数时，所求的百分比是差量÷(1+差量)×100%。

　　例3.有一瓶纯酒精，倒出1/4后用水加满，再倒出1/5后，用水加满，最后倒出1/6后用水加满，这时瓶中含有的纯酒精比原来少了几分之几?

　　解：以原来的纯酒精为整体“1”，则倒出1/4后瓶中剩下的纯酒精是原来的1-1/4=3/4;再倒出1/5后，瓶中剩下的纯酒精是原来的3/4×(1-1/5)=3/5;再倒出1/6后，瓶中剩下的纯酒精是原来的3/5×(1-1/6)=1/2;这时瓶中含有的纯酒精比原来少了1-1/2=1/2。

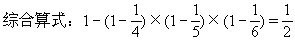
　　答：(略)

　　例4.某化肥厂生产一批化肥，计划用14天完成，由于改进了操作方法，提前4天完成了任务，求每天工作效率提高了百分之几。

　　解：设工作任务为“1”，则原来每天完成任务的1/14，后来每天完成全任务的1/(14-4)，这个差额占原来每天完成任务量的百分之几，就是提高的工作效率。即：

　　答：(略)

　　例6.某标准件厂制造一种螺丝，生产每个所需的时间由原来的6分钟减少了3.5分钟。过去每天生产80个，现在每天能超产百分之几?

　　解：这道题也可用比例解，工作时间一定，生产每个零件所用的时间与生产量成反比例。

　　设现在每天能生产X个。

　　现在每天能超产(192-80)÷80=140% 答：(略)

　　例7。水结成冰时，冰的体积比水增加1/11，当冰化成水时，水的体积比冰减少了几分之几?解：以水的体积为标准。冰的体积是水的：1+1/11=12/11，反过来以冰的体积为标准，水的体积是冰的：1÷12/11=11/12，所以当冰化成水时，水的体积比冰少了：1-11/12=1/12

　　综合算式：1-1÷(1+1/11)=1/12 答：(略)

　　例8.甲、乙、丙三人储蓄。甲储的钱数是乙的11/6倍，丙储的钱数是甲的2/5。那么乙和丙所储的钱数是甲的几分之几?

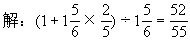
　　答：(略)